Lecture 6: Data modeling and linear regression
CME/STATS 195
Lan Huong Nguyen
October 16, 2018
Contents
Data Modeling
Linear Regression
Lasso Regression
Data Modeling
Introduction to models
“All models are wrong, but some are useful. Now it would be very remarkable if any system existing in the real world could be exactly represented by any simple model. However, cunningly chosen parsimonious models often do provide remarkably useful approximations (…). For such a model there is no need to ask the question”Is the model true?“. If”truth" is to be the “whole truth” the answer must be “No”. The only question of interest is “Is the model illuminating and useful?” – George E.P. Box, 1976
The goal of a model is to provide a simple low-dimensional summary of a dataset.
Models can be used to partition data into patterns of interest and residuals (other sources of variation and random noise).
Hypothesis generation vs. hypothesis confirmation
Usually models are used for inference or confirmation of a pre-specified hypothesis.
Doing inference correctly is hard. The key idea you must understand is that: Each observation can either be used for exploration or confirmation, NOT both.
Observation can be used many times for exploration, but only once for confirmation.
There is nothing wrong with exploration, but you should never sell an exploratory analysis as a confirmatory analysis because it is fundamentally misleading.
Confirmatory analysis
If you plan to do confirmatory analysis at some point after EDA, one approach is to split your data into three pieces before you begin the analysis:
Training set – the bulk (e.g. 60%) of the dataset which can be used to do anything: visualizing, fitting multiple models.
Validation set – a smaller set (e.g. 20%) used for manually comparing models and visualizations.
Test set – a set (e.g. 20%) held back used only ONCE to test and asses your final model.
Confirmatory analysis
Partitioning the dataset allows you to explore the training data, generate a number of candidate hypotheses and models.
You can select a final model based on its performance on the validation set.
Finally, when you are confident with the chosen model you can check how good it is using the test data.
Note that even when doing confirmatory modeling, you will still need to do EDA. If you don’t do any EDA you might remain blind to some quality problems with your data.
Model Basics
There are two parts to data modeling:
- defining a family of models: deciding on a set of models that can express a type of pattern you want to capture, e.g. a straight line, or a quadratic curve.
- fitting a model: finding a model within the family that the closest to your data.
A fitted model is just the best model from a chosen family of models, i.e. the “best” according to some set criteria.
This does not necessarily imply that the model is a good and certainly does NOT imply that the model is true.
The modelr package
The
modelrpackage, provides a few useful functions that are wrappers around base R’s modeling functions.These functions facilitate the data analysis process as they are nicely integrated with the
tidyversepipeline.modelris not automatically loaded when you load intidyversepackage, you need to do it separately:
library(modelr)A toy dataset
We will work with a simulated dataset sim1 from modelr:
sim1## # A tibble: 30 x 2
## x y
## <int> <dbl>
## 1 1 4.20
## 2 1 7.51
## 3 1 2.13
## 4 2 8.99
## 5 2 10.2
## 6 2 11.3
## 7 3 7.36
## 8 3 10.5
## 9 3 10.5
## 10 4 12.4
## # ... with 20 more rowsggplot(sim1, aes(x, y)) + geom_point()
Defining a family of models
The relationship between \(x\) and \(y\) for the points in sim1 look linear. So, will look for models which belong to a family of models of the following form:
\[y= \beta_0 + \beta_1 \cdot x\]
The models that can be expressed by the above formula, can adequately capture a linear trend.
We generate a few examples of the models from this family on the right.
models <- tibble(
b0 = runif(250, -20, 40),
b1 = runif(250, -5, 5))
ggplot(sim1, aes(x, y)) +
geom_abline(
data = models,
aes(intercept = b0, slope = b1),
alpha = 1/4) +
geom_point() 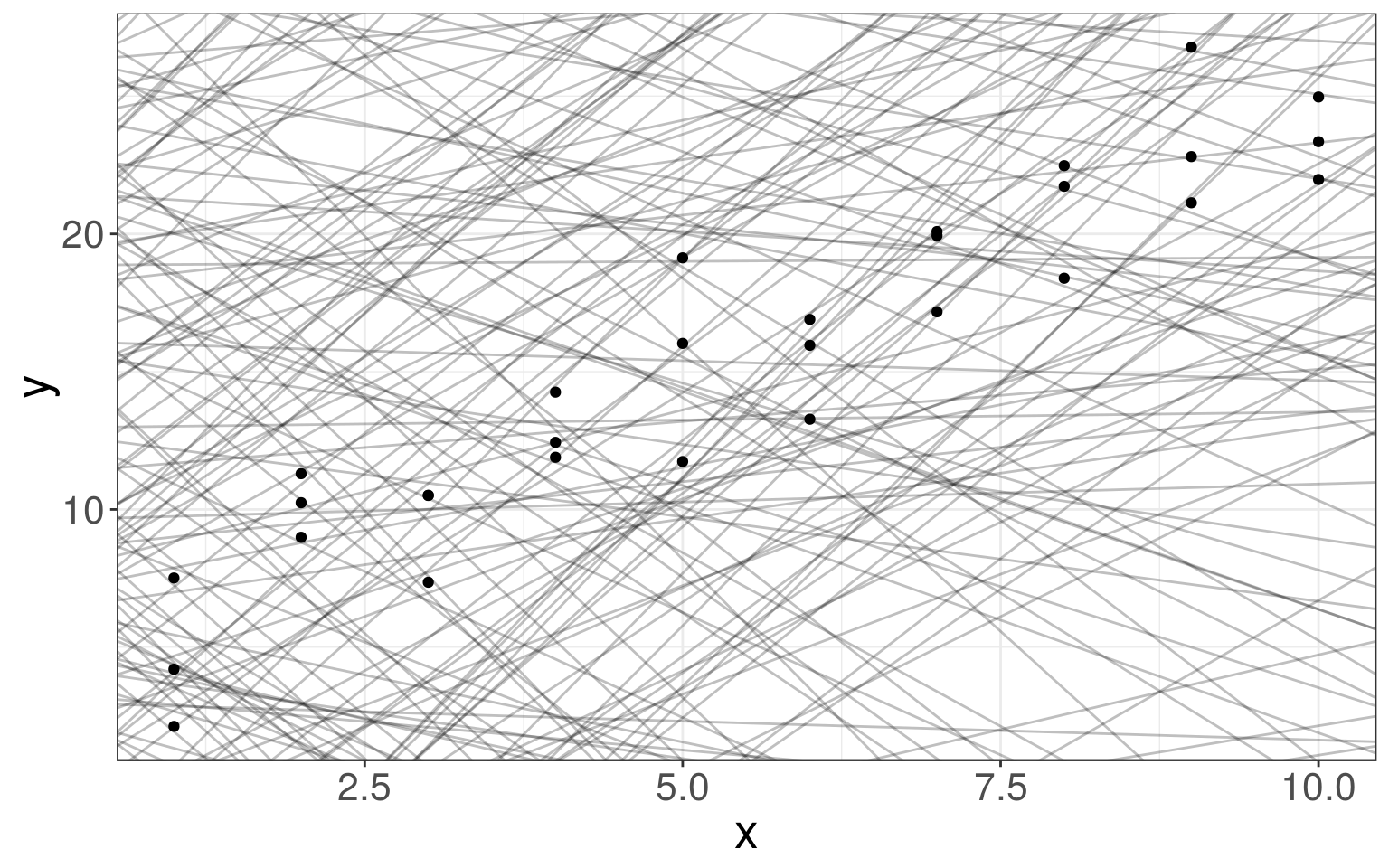
Fitting a model
From all the lines in the linear family of models, we need to find the best one, i.e. the one that is the closest to the data.
This means that we need to find parameters \(\hat a_0\) and \(\hat a_1\) that identify such a fitted line.
The closest to the data can be defined as the one with the minimum distance to the data points in the \(y\) direction (the minimum residuals):
\[\begin{align*} \|\hat e\|^2_2 &= \|\vec y - \hat y\|_2^2\\ &= \|\vec y - (\hat \beta_0 + \hat \beta_1 x)\|_2^2\\ &= \sum_{i = 1}^n (y_i - (\hat \beta_0 + \hat \beta_1 x_i))^2 \end{align*}\]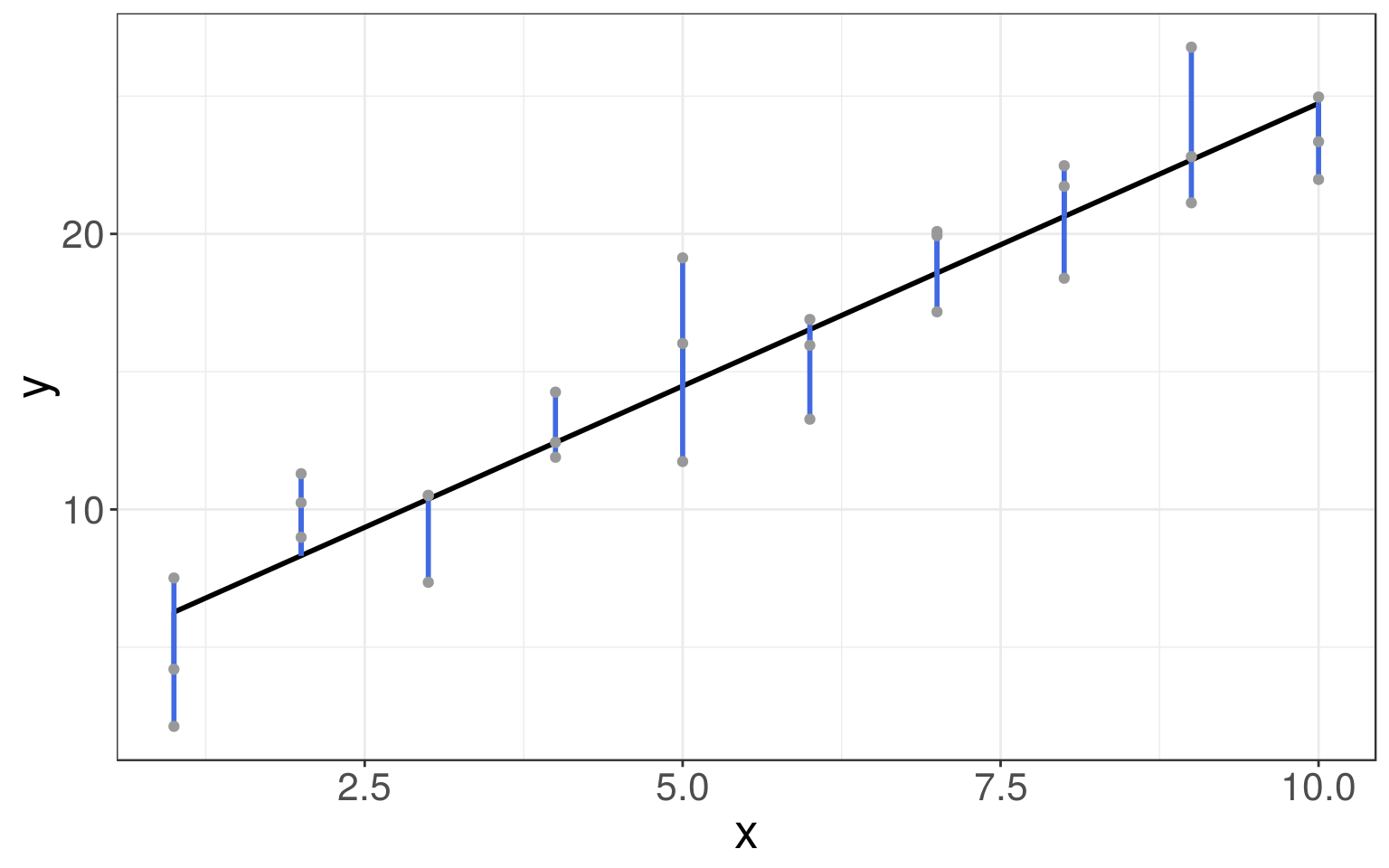
Linear Regression
Linear Regression
- Regression is a supervised learning method, whose goal is inferring the relationship between input data, \(x\), and a continuous response variable, \(y\).
- Linear regression is a type of regression where \(y\) is modeled as a linear function of \(x\).
- Simple linear regression predicts the output \(y\) from a single predictor \(x\). \[y = \beta_0 + \beta_1 x + \epsilon\]
- Multiple linear regression assumes \(y\) relies on many covariates: \[\begin{align*} y &= \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \dots + \beta_p x_p + \epsilon \\ &= \boldsymbol{\beta}^T \boldsymbol{x} + \epsilon \end{align*}\]
- here \(\epsilon\) denotes a random noise term with zero mean.
Objective function
Linear regression seeks a solution \(\hat y = \hat \beta \cdot \vec x\) that minimizes the difference between the true outcome \(y\) and the prediction \(\hat y\), in terms of the residual sum of squares (RSS).
\[ arg \min\limits_{\hat \beta} \sum_i \left(y_i - \boldsymbol{\hat \beta}^T \boldsymbol{x}_i\right)^2 \]
Simple Linear Regression
Predict the mileage per gallon using the weight of the car.
In R the linear models can be fit with a
lm()function.
# convert 'data.frame' to 'tibble':
mtcars <- tbl_df(mtcars)
# Separate the data into train and test:
set.seed(123)
n <- nrow(mtcars)
idx <- sample(1:n, size = floor(n/2))
mtcars_train <- mtcars[idx, ]
mtcars_test <- mtcars[-idx, ]
# Fit a simple linear model:
mtcars_fit <- lm(mpg ~ wt, mtcars_train)
# Extract the fitted model coefficients:
coef(mtcars_fit)## (Intercept) wt
## 36.469815 -5.406813# check the details on the fitted model:
summary(mtcars_fit)##
## Call:
## lm(formula = mpg ~ wt, data = mtcars_train)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.5302 -1.9952 0.0179 1.3017 3.5194
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 36.470 2.108 17.299 7.61e-11 ***
## wt -5.407 0.621 -8.707 5.04e-07 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.2 on 14 degrees of freedom
## Multiple R-squared: 0.8441, Adjusted R-squared: 0.833
## F-statistic: 75.81 on 1 and 14 DF, p-value: 5.043e-07Fitted values
We can compute the fitted values \(\hat y\), a.k.a. the predicted mpg values for existing observations using modelr::add_predictions() function.
mtcars_train <- mtcars_train %>% add_predictions(mtcars_fit)
mtcars_train## # A tibble: 16 x 12
## mpg cyl disp hp drat wt qsec vs am gear carb pred
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 19.2 6 168. 123 3.92 3.44 18.3 1 0 4 4 17.9
## 2 19.2 8 400 175 3.08 3.84 17.0 0 0 3 2 15.7
## 3 17.3 8 276. 180 3.07 3.73 17.6 0 0 3 3 16.3
## 4 27.3 4 79 66 4.08 1.94 18.9 1 1 4 1 26.0
## 5 26 4 120. 91 4.43 2.14 16.7 0 1 5 2 24.9
## 6 21 6 160 110 3.9 2.88 17.0 0 1 4 4 20.9
## 7 15.2 8 276. 180 3.07 3.78 18 0 0 3 3 16.0
## 8 15.2 8 304 150 3.15 3.44 17.3 0 0 3 2 17.9
## 9 15.8 8 351 264 4.22 3.17 14.5 0 1 5 4 19.3
## 10 17.8 6 168. 123 3.92 3.44 18.9 1 0 4 4 17.9
## 11 15.5 8 318 150 2.76 3.52 16.9 0 0 3 2 17.4
## 12 21.4 4 121 109 4.11 2.78 18.6 1 1 4 2 21.4
## 13 13.3 8 350 245 3.73 3.84 15.4 0 0 3 4 15.7
## 14 15 8 301 335 3.54 3.57 14.6 0 1 5 8 17.2
## 15 30.4 4 95.1 113 3.77 1.51 16.9 1 1 5 2 28.3
## 16 10.4 8 460 215 3 5.42 17.8 0 0 3 4 7.14Predictions for new observations
To predict the mpg for new observations, e.g. cars not in the dataset, we first need to generate a data table with predictors \(x\), in this case the car weights:
newcars <- tibble(wt = c(2, 2.1, 3.14, 4.1, 4.3))
newcars <- newcars %>% add_predictions(mtcars_fit)
newcars## # A tibble: 5 x 2
## wt pred
## <dbl> <dbl>
## 1 2 25.7
## 2 2.1 25.1
## 3 3.14 19.5
## 4 4.1 14.3
## 5 4.3 13.2Predictions for the test set
Remember that we already set aside a test set check our model:
mtcars_test <- mtcars_test %>% add_predictions(mtcars_fit)
head(mtcars_test, 3)## # A tibble: 3 x 12
## mpg cyl disp hp drat wt qsec vs am gear carb pred
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 21 6 160 110 3.9 2.62 16.5 0 1 4 4 22.3
## 2 22.8 4 108 93 3.85 2.32 18.6 1 1 4 1 23.9
## 3 21.4 6 258 110 3.08 3.22 19.4 1 0 3 1 19.1Compute the root mean square error:
\[ RMSE = \frac{1}{\sqrt{n}}\|\vec{y} - \vec{\hat y}\| = \sqrt{\frac{1}{n}\sum_{i = 1}^n(y_i - \hat y_i)^2} \]
sqrt(mean((mtcars_test$mpg - mtcars_test$pred)^2))## [1] 3.902534Visualizing the model
Now we can compare our predictions (grey) to the observed (black) values.
ggplot(mtcars_train, aes(wt)) + geom_point(aes(y = mpg)) +
geom_line(aes(y = pred), color = "red", size = 1) +
geom_point(aes(y = pred), fill = "grey", color = "black", shape = 21, size = 2) 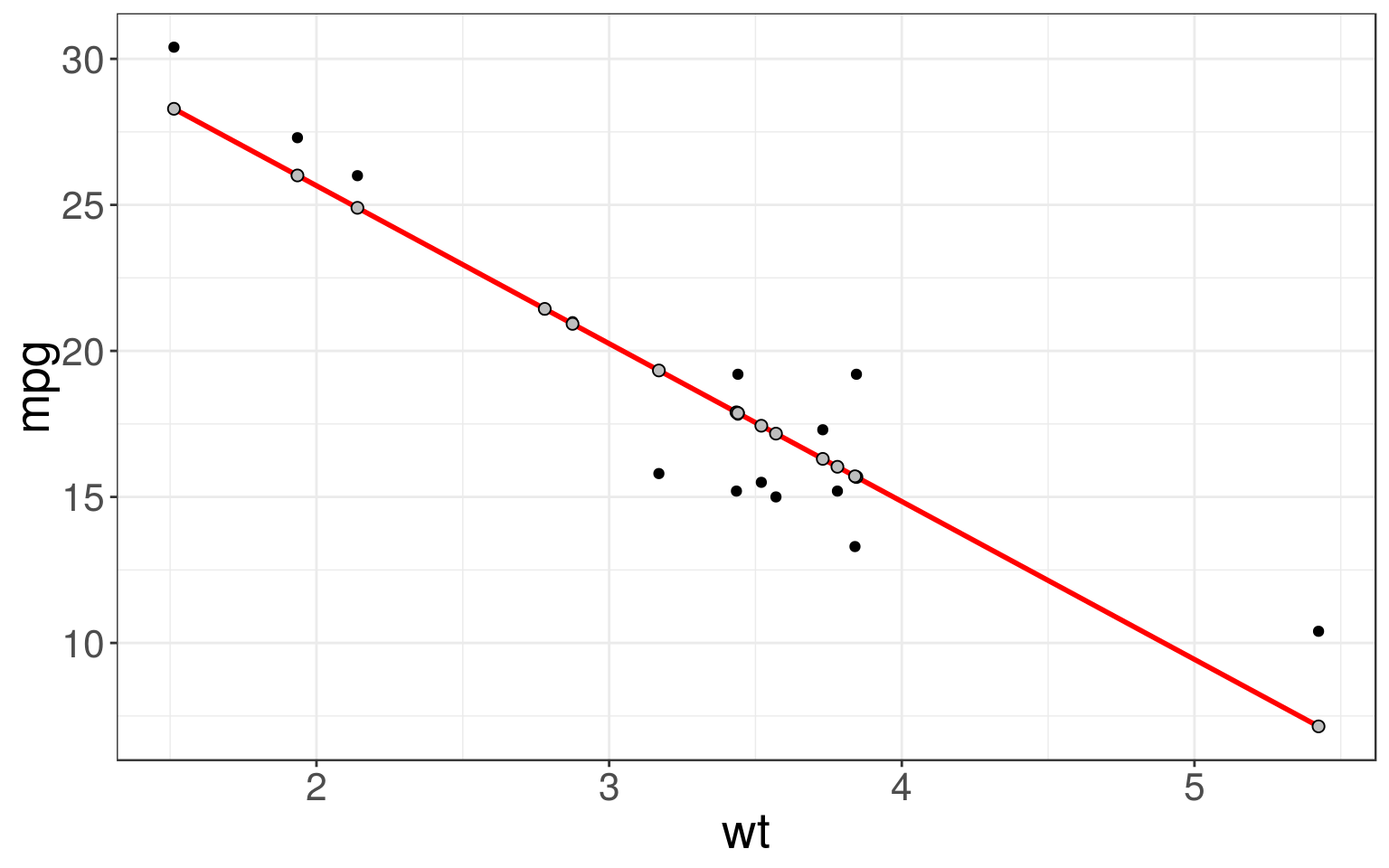
Visualizing the residuals
The residuals tell you what the model has missed. We can compute and add residuals to data with add_residuals() from modelr package:
Plotting residuals is a good practice – you want the residuals to look like random noise.
mtcars_train <- mtcars_train %>%
add_residuals(mtcars_fit)
mtcars_train %>%
select(mpg, mpg, resid, pred)## # A tibble: 16 x 3
## mpg resid pred
## <dbl> <dbl> <dbl>
## 1 19.2 1.33 17.9
## 2 19.2 3.52 15.7
## 3 17.3 0.998 16.3
## 4 27.3 1.29 26.0
## 5 26 1.10 24.9
## 6 21 0.0748 20.9
## 7 15.2 -0.832 16.0
## 8 15.2 -2.70 17.9
## 9 15.8 -3.53 19.3
## 10 17.8 -0.0704 17.9
## 11 15.5 -1.94 17.4
## 12 21.4 -0.0389 21.4
## 13 13.3 -2.41 15.7
## 14 15 -2.17 17.2
## 15 30.4 2.11 28.3
## 16 10.4 3.26 7.14ggplot(mtcars_train, aes(wt, resid)) +
geom_ref_line(h = 0, colour = "grey") +
geom_point() 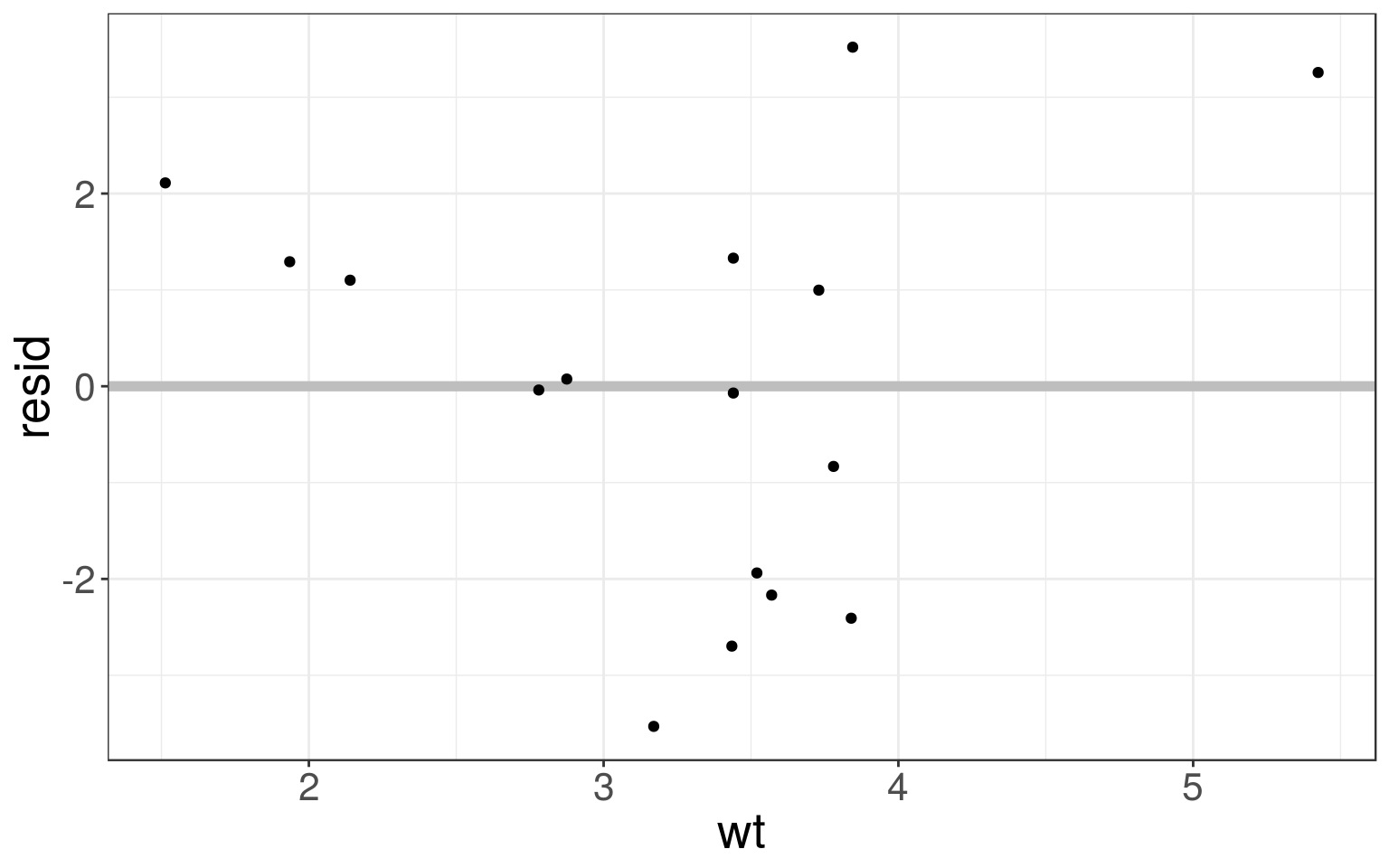
Formulae in R
You have seen that lm() takes in a formula relation y ~ x as an argument.
You can take a look at what R actually does, you can use the model_matrix().
sim1## # A tibble: 30 x 3
## x y pred
## <int> <dbl> <dbl>
## 1 1 4.20 6.27
## 2 1 7.51 6.27
## 3 1 2.13 6.27
## 4 2 8.99 8.32
## 5 2 10.2 8.32
## 6 2 11.3 8.32
## 7 3 7.36 10.4
## 8 3 10.5 10.4
## 9 3 10.5 10.4
## 10 4 12.4 12.4
## # ... with 20 more rowsmodel_matrix(sim1, y ~ x)## # A tibble: 30 x 2
## `(Intercept)` x
## <dbl> <dbl>
## 1 1 1
## 2 1 1
## 3 1 1
## 4 1 2
## 5 1 2
## 6 1 2
## 7 1 3
## 8 1 3
## 9 1 3
## 10 1 4
## # ... with 20 more rowsFormulae with categorical variables
It doesn’t make sense to parametrize the model with categorical variables, as we did before.
transvariable is not a number, so R creates an indicator column that is 1 if “male”, and 0 if “female”.
(df <- tibble(
sex = c("male", "female", "female",
"female", "male", "male"),
response = c(2, 5, 1, 3, 6, 8)
))## # A tibble: 6 x 2
## sex response
## <chr> <dbl>
## 1 male 2
## 2 female 5
## 3 female 1
## 4 female 3
## 5 male 6
## 6 male 8model_matrix(df, response ~ sex)## # A tibble: 6 x 2
## `(Intercept)` sexmale
## <dbl> <dbl>
## 1 1 1
## 2 1 0
## 3 1 0
## 4 1 0
## 5 1 1
## 6 1 1- In general, it creates k−1 columns, where k is the number of categories.
(df <- tibble(
rating = c("good", "bad", "average", "bad",
"average", "good", "bad", "good"),
score = c(2, 5, 1, 3, 6, 8, 10, 6)
))## # A tibble: 8 x 2
## rating score
## <chr> <dbl>
## 1 good 2
## 2 bad 5
## 3 average 1
## 4 bad 3
## 5 average 6
## 6 good 8
## 7 bad 10
## 8 good 6model_matrix(df, score ~ rating)## # A tibble: 8 x 3
## `(Intercept)` ratingbad ratinggood
## <dbl> <dbl> <dbl>
## 1 1 0 1
## 2 1 1 0
## 3 1 0 0
## 4 1 1 0
## 5 1 0 0
## 6 1 0 1
## 7 1 1 0
## 8 1 0 1But you don’t need to worry about the parametrization to make predictions.
Multiple Linear Regression
Models often include multiple predictors, e.g. we might like to predict mpg using three variables: wt, disp and cyl.
ggplot(mtcars, aes(x=wt, y=mpg, col=cyl, size=disp)) +
geom_point() +
scale_color_viridis_c()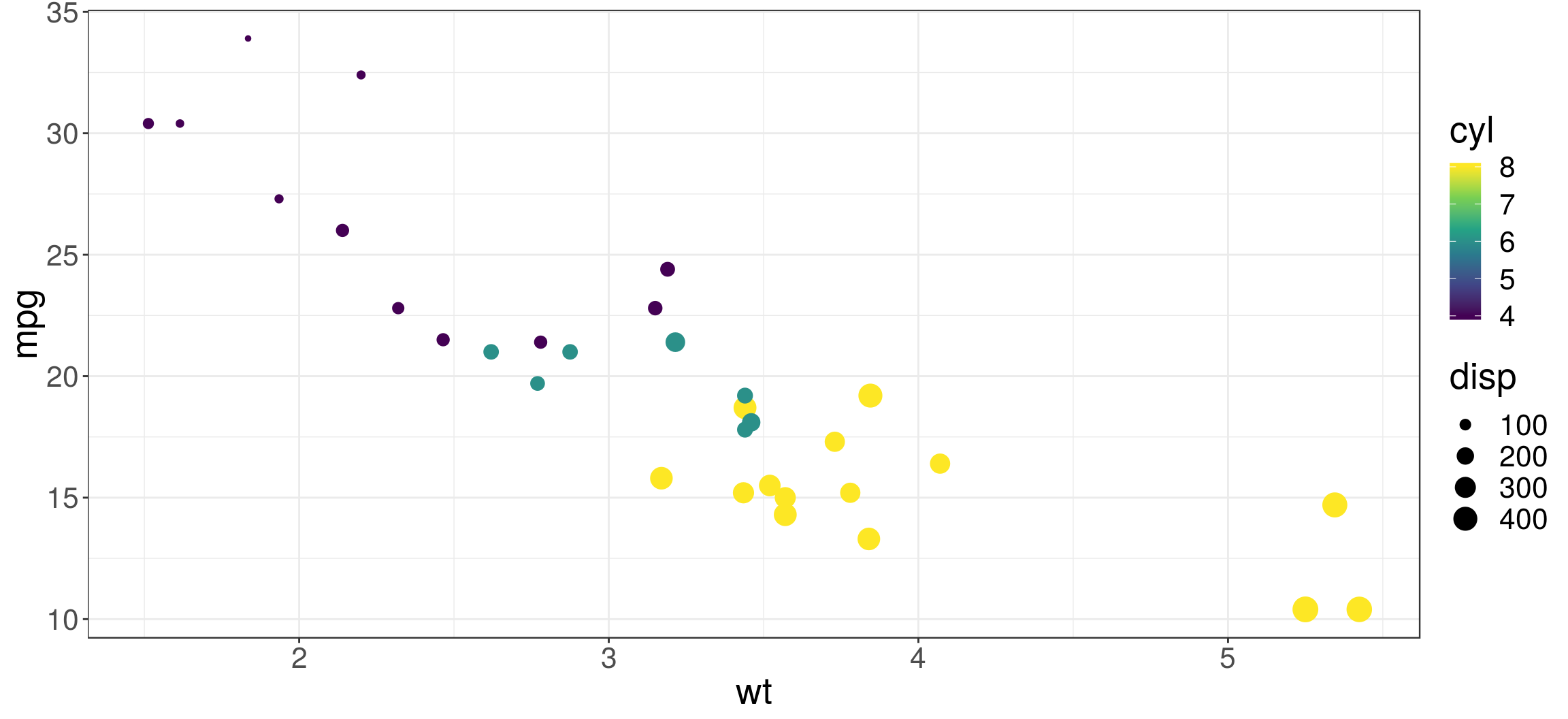
mtcars_mult_fit <- lm(mpg ~ wt + disp + cyl, data = mtcars_train)
# Summarize the results
summary(mtcars_mult_fit)##
## Call:
## lm(formula = mpg ~ wt + disp + cyl, data = mtcars_train)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.4016 -0.9539 0.0017 0.6243 3.4510
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 40.259994 2.692593 14.952 4.03e-09 ***
## wt -3.986230 0.984659 -4.048 0.00162 **
## disp 0.009933 0.010756 0.924 0.37394
## cyl -1.644638 0.629635 -2.612 0.02272 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.818 on 12 degrees of freedom
## Multiple R-squared: 0.9088, Adjusted R-squared: 0.886
## F-statistic: 39.88 on 3 and 12 DF, p-value: 1.616e-06To predict mpg for new cars, you must first create a data frame describing the attributes of the new cars, before computing predicted mpg values.
newcars <- expand.grid(
wt = c(2.1, 3.6, 5.1),
disp = c(150, 250),
cyl = c(4, 6)
)
newcars## wt disp cyl
## 1 2.1 150 4
## 2 3.6 150 4
## 3 5.1 150 4
## 4 2.1 250 4
## 5 3.6 250 4
## 6 5.1 250 4
## 7 2.1 150 6
## 8 3.6 150 6
## 9 5.1 150 6
## 10 2.1 250 6
## 11 3.6 250 6
## 12 5.1 250 6newcars <- newcars %>%
add_predictions(mtcars_mult_fit)
newcars## wt disp cyl pred
## 1 2.1 150 4 26.80031
## 2 3.6 150 4 20.82097
## 3 5.1 150 4 14.84162
## 4 2.1 250 4 27.79361
## 5 3.6 250 4 21.81427
## 6 5.1 250 4 15.83492
## 7 2.1 150 6 23.51104
## 8 3.6 150 6 17.53169
## 9 5.1 150 6 11.55235
## 10 2.1 250 6 24.50434
## 11 3.6 250 6 18.52499
## 12 5.1 250 6 12.54565Predictions for the test set
mtcars_test_mult <- mtcars_test %>% add_predictions(mtcars_mult_fit)
head(mtcars_test_mult, 3)## # A tibble: 3 x 12
## mpg cyl disp hp drat wt qsec vs am gear carb pred
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 21 6 160 110 3.9 2.62 16.5 0 1 4 4 21.5
## 2 22.8 4 108 93 3.85 2.32 18.6 1 1 4 1 25.5
## 3 21.4 6 258 110 3.08 3.22 19.4 1 0 3 1 20.1Compute the root mean square error:
\[ RMSE = \frac{1}{\sqrt{n}}\|\vec{y} - \vec{\hat y}\| = \sqrt{\frac{1}{n}\sum_{i = 1}^n(y_i - \hat y_i)^2} \]
sqrt(mean((mtcars_test_mult$mpg - mtcars_test_mult$pred)^2))## [1] 3.172103Interaction terms
An interaction occurs when an independent variable has a different effect on the outcome depending on the values of another independent. variable.
For example, one variable, \(x_1\) might have a different effect on \(y\) within different categories or groups, given by variable \(x_2\).
If you are not familiar with the concept of the interaction terms, read this.
Formulas with interactions
In the sim3 dataset, there is a categorical, x2, and a continuous, x1, predictor.
ggplot(sim3, aes(x=x1, y=y)) + geom_point(aes(color = x2)) 
Models with interactions
We could fit two different models, one without and one with (mod2) different slopes and intercepts for each line (for each x2 category).
# Model without interactions:
mod1 <- lm(y ~ x1 + x2, data = sim3)
# Model with interactions:
mod2 <- lm(y ~ x1 * x2, data = sim3)
# Generate a data grid for two variables
# and compute predictions from both models
grid <- sim3 %>% data_grid(x1, x2) %>%
gather_predictions(mod1, mod2)
head(grid, 3)## # A tibble: 3 x 4
## model x1 x2 pred
## <chr> <int> <fct> <dbl>
## 1 mod1 1 a 1.67
## 2 mod1 1 b 4.56
## 3 mod1 1 c 6.48tail(grid, 3)## # A tibble: 3 x 4
## model x1 x2 pred
## <chr> <int> <fct> <dbl>
## 1 mod2 10 b -0.162
## 2 mod2 10 c 5.48
## 3 mod2 10 d 3.98ggplot(sim3, aes(x=x1, y=y, color=x2)) +
geom_point() +
geom_line(data=grid, aes(y=pred)) +
facet_wrap(~ model) 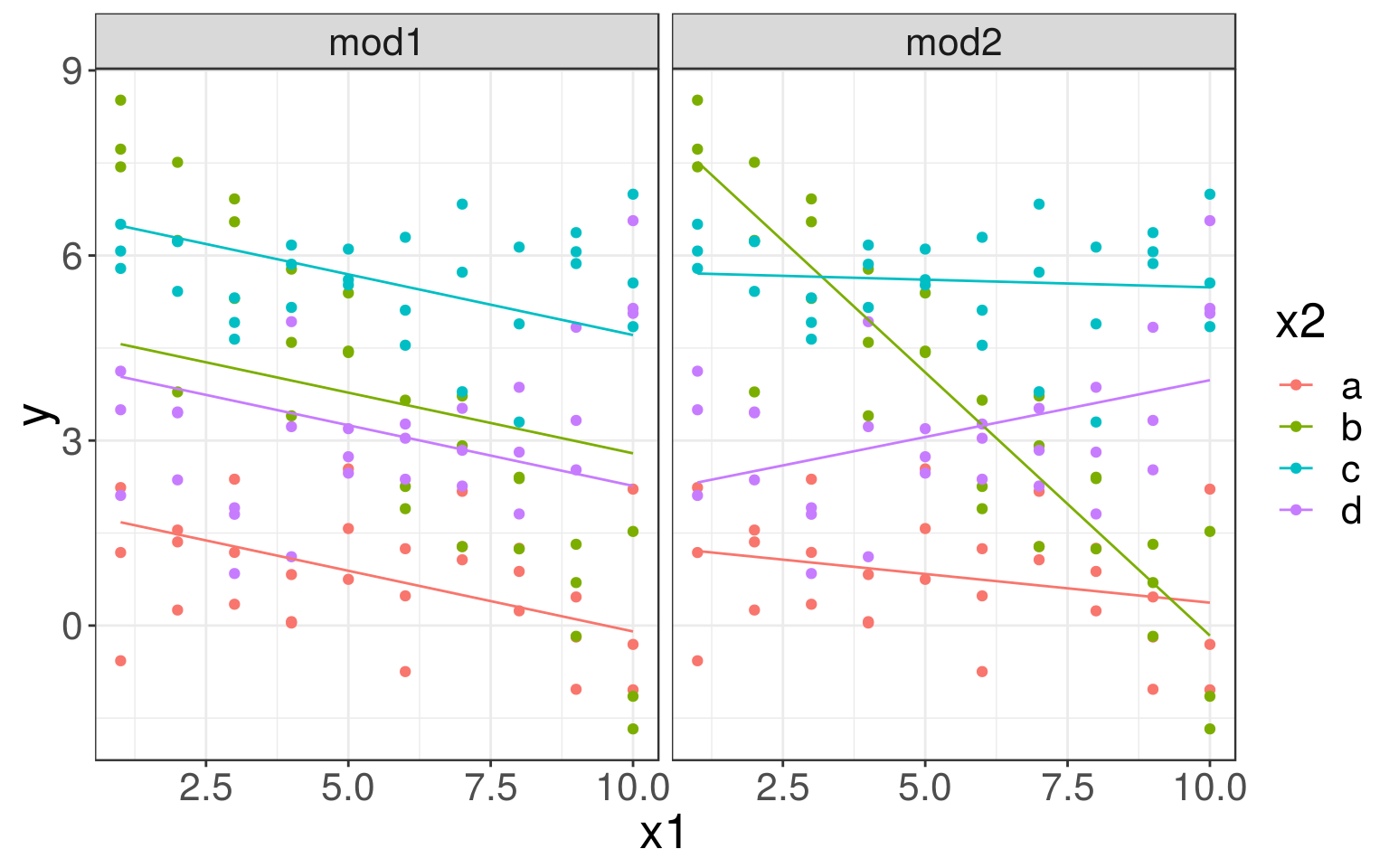
Now, we fit interaction effects for the mtcars dataset. Note the ‘:’-notation for the interaction term.
mfit_inter <- lm(mpg ~ am * wt, mtcars_train)
names(coefficients(mfit_inter))## [1] "(Intercept)" "am" "wt" "am:wt"summary(mfit_inter)##
## Call:
## lm(formula = mpg ~ am * wt, data = mtcars_train)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.5603 -1.0064 0.0679 0.7265 3.3565
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 28.7955 3.7796 7.619 6.18e-06 ***
## am 13.7636 4.5621 3.017 0.01072 *
## wt -3.3685 0.9759 -3.452 0.00479 **
## am:wt -4.4730 1.3701 -3.265 0.00677 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.721 on 12 degrees of freedom
## Multiple R-squared: 0.9183, Adjusted R-squared: 0.8978
## F-statistic: 44.94 on 3 and 12 DF, p-value: 8.43e-07Exercise 1
Go to the “Lec6_Exercises.Rmd” file, which can be downloaded from the class website under the Lecture tab.
Complete Exercise 1.
Lasso Regression
Choosing a model
- Modern datasets often have “too” many variables, e.g. predict the risk of a disease from the single nucleotide polymorphisms (SNPs) data.
- Issue: \(n \ll p\) i.e. no. of predictors is much larger than than the no. of observations.
- Lasso regression is especially useful for problems, where
the number of available covariates is extremely large, but only a handful of them are relevant for the prediction of the outcome.
Lasso Regression
- Lasso regression is simply regression with \(L_1\) penalty.
- That is, it solves the problem:
\[\boldsymbol{\hat \beta} = arg \min\limits_{\boldsymbol{\beta}} \sum_i \left(y^{(i)} - \boldsymbol{\beta}^T \boldsymbol{x}^{(i)}\right)^2 + \lambda \|\boldsymbol{\beta}\|_1\]
It turns out that the \(L_1\) norm \(\|\vec \beta\|_1 = \sum_i |beta_i|\) promotes sparsity, i.e. only a handful of \(\hat\beta_i\) will actually be non-zero.
The number of non-zero coefficients depends on the choice of the tuning parameter, \(\lambda\). The higher the \(\lambda\) the fewer non-zero coefficients.
glmnet
- Lasso regression is implemented in an R package
glmnet. - An introductory tutorial to the package can be found here.
# install.packages("glmnet")
library(glmnet)- We go back to
mtcarsdatasets and use Lasso regression to predict thempgusing all variables. - Lasso will pick a subset of predictors that best predict the
mpg. - This means that we technically allow for all variables to be included, but due to penalization, most of the fitted coefficients will be zero.
mtcars <- as.data.frame(mtcars)
class(mtcars)## [1] "data.frame"head(mtcars)## mpg cyl disp hp drat wt qsec vs am gear carb
## Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4
## Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4
## Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1
## Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1
## Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2
## Valiant 18.1 6 225 105 2.76 3.460 20.22 1 0 3 1Fitting a sparse model
# Convert to 'glmnet' required input format:
y <- mtcars[, 1] # response vector, 'mpg'
X <- mtcars[, -1] # all other variables treated as predictors
X <- data.matrix(X, "matrix") # converts to NUMERIC matrix
# Choose a training set
set.seed(123)
idx <- sample(1:nrow(mtcars), floor(0.7 * nrow(mtcars)))
X_train <- X[idx, ]; y_train <- y[idx]
X_test <- X[-idx, ]; y_test <- y[-idx]
# Fit a sparse model
fit <- glmnet(X_train, y_train)
names(fit)## [1] "a0" "beta" "df" "dim" "lambda"
## [6] "dev.ratio" "nulldev" "npasses" "jerr" "offset"
## [11] "call" "nobs"glmnet()compute the Lasso regression for a sequence of different tuning parameters, \(\lambda\).- Each row of
print(fit)corresponds to a particular \(\lambda\) in the sequence. - column
Dfdenotes the number of non-zero coefficients (degrees of freedom), %Devis the percentage variance explained,Lambdais the value of the currently chosen tuning parameter.
print(fit)##
## Call: glmnet(x = X_train, y = y_train)
##
## Df %Dev Lambda
## [1,] 0 0.0000 4.679000
## [2,] 1 0.1383 4.264000
## [3,] 2 0.2626 3.885000
## [4,] 2 0.3700 3.540000
## [5,] 2 0.4593 3.225000
## [6,] 2 0.5333 2.939000
## [7,] 2 0.5948 2.678000
## [8,] 2 0.6459 2.440000
## [9,] 2 0.6883 2.223000
## [10,] 2 0.7235 2.026000
## [11,] 2 0.7527 1.846000
## [12,] 2 0.7770 1.682000
## [13,] 3 0.7993 1.532000
## [14,] 3 0.8179 1.396000
## [15,] 3 0.8335 1.272000
## [16,] 3 0.8463 1.159000
## [17,] 3 0.8570 1.056000
## [18,] 3 0.8659 0.962300
## [19,] 3 0.8733 0.876800
## [20,] 4 0.8797 0.798900
## [21,] 4 0.8862 0.727900
## [22,] 4 0.8915 0.663300
## [23,] 4 0.8960 0.604300
## [24,] 4 0.8997 0.550700
## [25,] 4 0.9028 0.501700
## [26,] 4 0.9054 0.457200
## [27,] 4 0.9075 0.416600
## [28,] 4 0.9093 0.379500
## [29,] 5 0.9108 0.345800
## [30,] 6 0.9124 0.315100
## [31,] 5 0.9139 0.287100
## [32,] 5 0.9152 0.261600
## [33,] 5 0.9162 0.238400
## [34,] 5 0.9171 0.217200
## [35,] 5 0.9178 0.197900
## [36,] 5 0.9184 0.180300
## [37,] 5 0.9189 0.164300
## [38,] 5 0.9193 0.149700
## [39,] 4 0.9197 0.136400
## [40,] 4 0.9199 0.124300
## [41,] 4 0.9201 0.113200
## [42,] 4 0.9203 0.103200
## [43,] 5 0.9215 0.094020
## [44,] 7 0.9263 0.085660
## [45,] 7 0.9313 0.078050
## [46,] 6 0.9350 0.071120
## [47,] 6 0.9361 0.064800
## [48,] 6 0.9371 0.059050
## [49,] 7 0.9379 0.053800
## [50,] 7 0.9387 0.049020
## [51,] 8 0.9396 0.044670
## [52,] 9 0.9414 0.040700
## [53,] 10 0.9443 0.037080
## [54,] 10 0.9473 0.033790
## [55,] 10 0.9499 0.030790
## [56,] 10 0.9520 0.028050
## [57,] 10 0.9538 0.025560
## [58,] 10 0.9553 0.023290
## [59,] 10 0.9565 0.021220
## [60,] 10 0.9575 0.019330
## [61,] 10 0.9584 0.017620
## [62,] 10 0.9591 0.016050
## [63,] 10 0.9597 0.014630
## [64,] 10 0.9602 0.013330
## [65,] 10 0.9606 0.012140
## [66,] 10 0.9609 0.011060
## [67,] 10 0.9612 0.010080
## [68,] 10 0.9614 0.009186
## [69,] 10 0.9616 0.008369
## [70,] 10 0.9618 0.007626
## [71,] 10 0.9619 0.006949
## [72,] 10 0.9620 0.006331
## [73,] 10 0.9621 0.005769
## [74,] 10 0.9622 0.005256
## [75,] 10 0.9623 0.004789
## [76,] 10 0.9623 0.004364
## [77,] 10 0.9624 0.003976
## [78,] 10 0.9624 0.003623
## [79,] 10 0.9625 0.003301
## [80,] 10 0.9625 0.003008
## [81,] 10 0.9625 0.002741
## [82,] 10 0.9625 0.002497
## [83,] 10 0.9626 0.002275
## [84,] 10 0.9626 0.002073
## [85,] 10 0.9626 0.001889
## [86,] 10 0.9626 0.001721
## [87,] 10 0.9626 0.001568# label = TRUE makes the plot annotate the curves with the corresponding coeffients labels.
plot(fit, label = TRUE, xvar = "lambda") 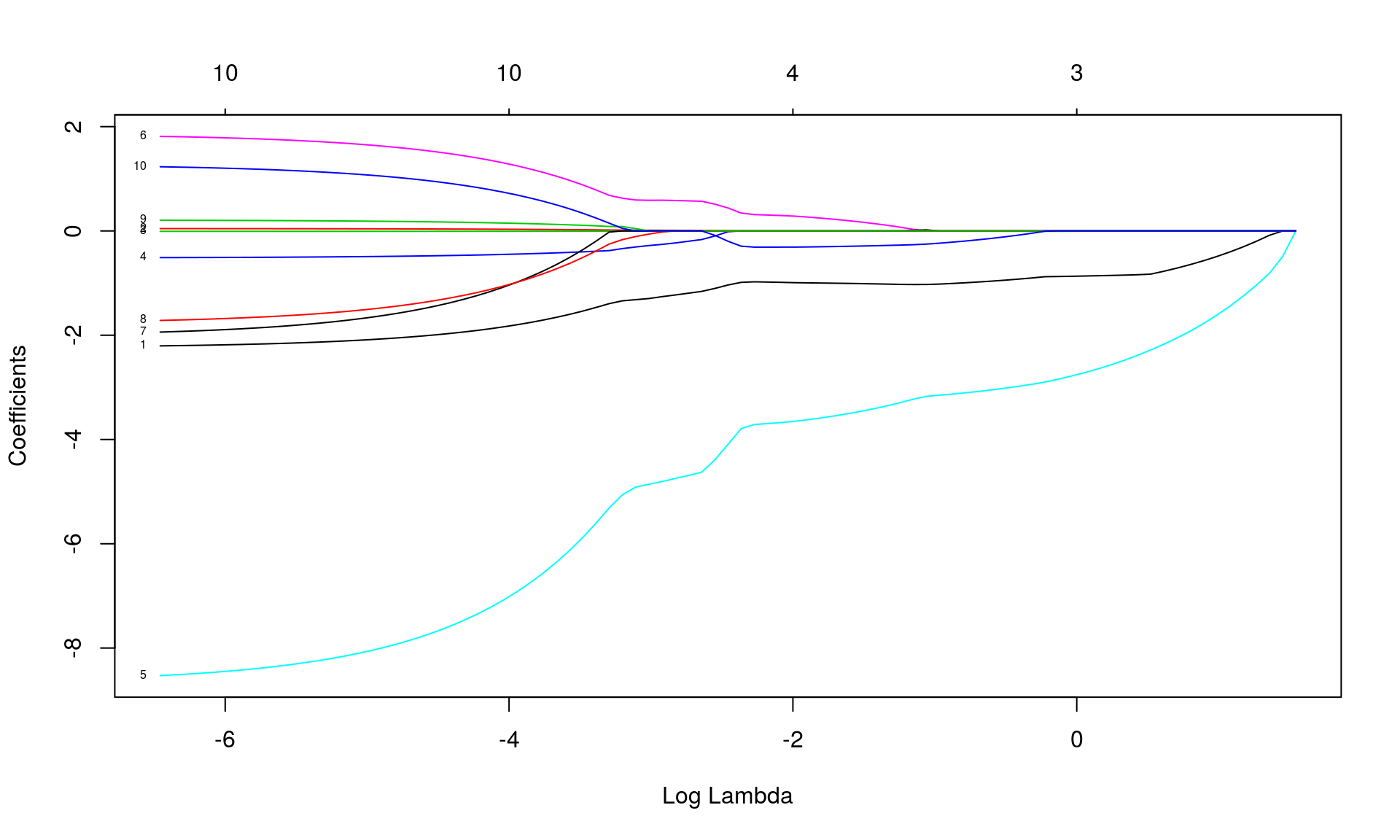
- the y-axis corresponds the value of the coefficients.
- the x-axis is denoted “Log Lambda” corresponds to the value of \(\lambda\) parameter penalizing the L1 norm of \(\boldsymbol{ \hat \beta}\)
- Each curve corresponds to a single variable, and shows the value of the coefficient as the tuning parameter varies.
- \(\|\hat \beta\|_{L_1}\) increases and \(\lambda\) decreases from left to right.
- When \(\lambda\) is small (right) there are more non-zero coefficients.
The computed Lasso coefficient for a particular choice of \(\lambda\) can be printed using:
# Lambda = 1
coef(fit, s = 1)## 11 x 1 sparse Matrix of class "dgCMatrix"
## 1
## (Intercept) 34.877093111
## cyl -0.867649618
## disp .
## hp -0.005778702
## drat .
## wt -2.757808266
## qsec .
## vs .
## am .
## gear .
## carb .- Like for
lm(), we can use a functionpredict()to predict thempgfor the training or the test data. - However, we need specify the value of \(\lambda\) using the argument
s.
# Predict for the test set:
predict(fit, newx = X_test, s = c(0.5, 1.5, 2))## 1 2 3
## Datsun 710 25.36098 23.87240 23.22262
## Valiant 19.82245 19.42427 19.41920
## Duster 360 16.19324 17.27111 17.74858
## Merc 230 22.62471 21.86937 21.50396
## Merc 450SE 15.20595 16.16123 16.71324
## Cadillac Fleetwood 11.25687 13.28117 14.26985
## Chrysler Imperial 10.81730 13.01570 14.07314
## Fiat 128 25.88928 24.20103 23.47110
## Toyota Corolla 27.01880 25.08206 24.22690
## Toyota Corona 24.89106 23.51713 22.92237Each of the columns corresponds to a choice of \(\lambda\).
Choosing \(\lambda\)
- To choose \(\lambda\) can use cross-validation.
- Use
cv.glmnet()function to perform a k-fold cross validation.
In k-fold cross-validation, the original sample is randomly partitioned into k equal sized subsamples. Of the k subsamples, a single subsample is retained as the validation data for testing the model, and the remaining k − 1 subsamples are used as training data. 1
set.seed(1)
# `nfolds` argument sets the number of folds (k).
cvfit <- cv.glmnet(X_train, y_train, nfolds = 5)
plot(cvfit)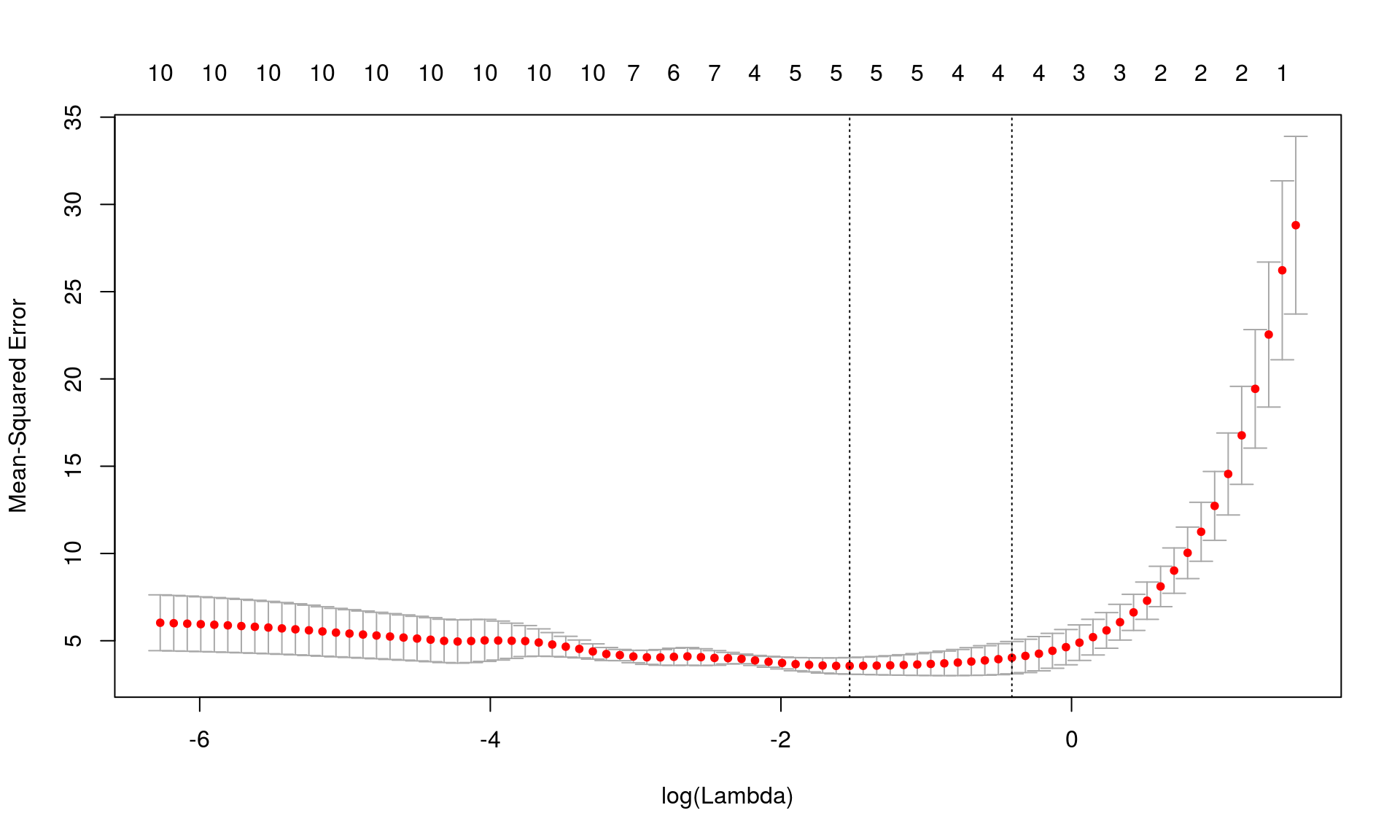
- The red dots are the average MSE over the k-folds.
- The two chosen \(\lambda\) values are the one with \(MSE_{min}\) and one with \(MSE_{min} + sd_{min}\)
\(\lambda\) with minimum mean squared error, MSE:
cvfit$lambda.min## [1] 0.2171905The “best” \(\lambda\) in a practical sense is usually chosen to be the biggest \(\lambda\) whose MSE is within one standard error of the minimum MSE.
cvfit$lambda.1se## [1] 0.6632685Predictions using the “best” \(\lambda\):
final_pred <- predict(cvfit, newx=X_test, s="lambda.1se")
final_pred## 1
## Datsun 710 25.01062
## Valiant 19.68422
## Duster 360 16.32664
## Merc 230 22.44375
## Merc 450SE 15.35370
## Cadillac Fleetwood 11.58909
## Chrysler Imperial 11.13782
## Fiat 128 25.54984
## Toyota Corolla 26.64431
## Toyota Corona 24.55160More on models
Building Models
Building models is an important part of EDA.
It takes practice to gain an intuition for which patterns to look for and what predictors to select that are likely to have an important effect.
You should go over examples in http://r4ds.had.co.nz/model-building.html to see concrete examples of how a model is built for diamonds and nycflights2013 datasets we have seen before.
Other model families
This chapter has focused exclusively on the class of linear models \[ y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \dots + \beta_p x_p + \epsilon = \vec \beta \vec x + \epsilon \]
and penalized linear models.
There are a large set of other model classes.
Extensions of linear models:
- Generalized linear models,
stats::glm(), binary or count data. - Generalized additive models,
mgcv::gam(), extend generalized linear models to incorporate arbitrary smooth functions. - Robust linear models,
MASS:rlm(), less sensitive to outliers.
Completely different models:
- Trees,
rpart::rpart(), fit a piece-wise constant model splitting the data into progressively smaller and smaller pieces. - Random forests,
randomForest::randomForest(), aggregate many different trees. - Gradient boosting machines,
xgboost::xgboost(), aggregate trees.
Useful Books
“An introduction to Statistical Learning” [ISL] by James, Witten, Hastie and Tibshirani
“Elements of statistical learning” [ESL] by Hastie, Tibshirani and Friedman
“Introduction to Linear Regression Analysis” by Montgomery, Peck, Vinning